"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

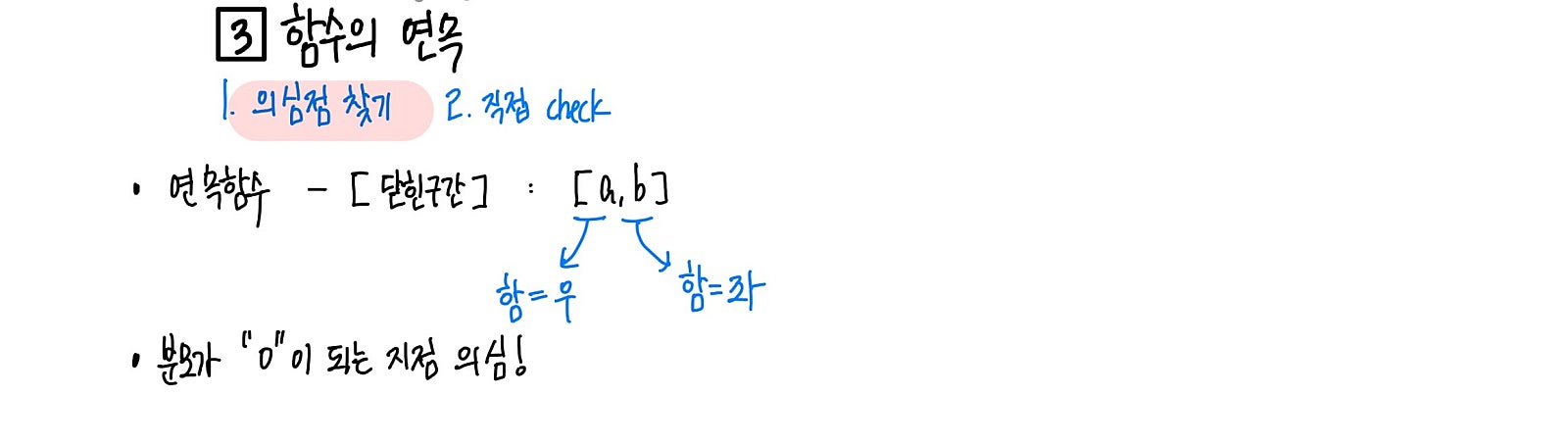
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
제발
-
노래 좋네요
-
그러면 정말정말 고맙겟어오...
-
그땐 미쳐 알지못했지…
-
센츄리온 2
내일 나오나요??????
-
재수할 땐 쳐다보기도 싫었음 다시 들어보니까 좋네
-
3년 내신 총합 1.27 6월 11222 9월 11112 수능 21225 최저용으로...
-
마 자신있음 들어온나
-
설의훌리는 아님.. 진짜 궁금해서
-
ㅈㄱㄴ 인터넷에는 pdf밖에 없길래 올려용 문제 배치는 가나형때처럼 1~21 / 22~30로 해놨음
-
바지 글보고 예전에 만족스럽게 산 바지 찾아보려 다시들어갔는데 ㄷ;
-
현역 기하 커리 2
지금은 시발점 본교재로만 공부하고있는데 이거 다 하면 기출로 바로 가야할까요?
-
고점매수에 단단히 물린 기분인데 타과 애들 시간표 짠다 엠티간다 하다못해 단톡방...
-
부엉이가 되자 0
외대생이 되는거야
-
임정환 풀커리에 현돌 기시감이나 유명한 모의고사 하면 되나요?
-
ㄹㅇ 개민폐니까 여기 혹시 그런 사람잇르면 자제좀요.
-
투표부탁드려요
-
재수 고민 0
언미영물1지1 96 97 2 3컷 3컷 시대재종 vs 시대 단과(라이브)듣고 재수...
-
윤도영t가 쁘띠한 드레스 입은거 생각나잖아..
-
이래서야 밥을 이때 먹을수밖에 없잖아
-
"평가원스럽지 않음" 심심하면 풀어보세요 최초 정답자 10,000 XDK
-
당신은 해변의 여자 하지만 너 없이 난 해변의 환자~~~~~
-
사랑에 난 빠져버렸어 혼자인 게 좋아 나를 사랑했던 나에게
-
허락도 안 받았는데 되겠냐고 ㅋㅋㅋㅋ 1도 안 궁금함
-
이 책 잼있네요 올비분들은 어떤단어책 외우시나요???
-
있나요
-
야ㄷ코리아 걔 맞음ㅋㅋ 시청자 차면 시작한댕 https://url1.io/KONnw
-
랩만 안했으면 좋겠음 마마봤는데 못봐줄정도로 오글거림
-
사탐런으로 서울대 자전 가기 vs 투투런으로 서울대 수학과 / 수학교육과 가기 2
어느게 더 빡셀까요
-
박광일질문 1
한번들어보고맘에들면 커리타려고하는데 조정식이 올해 11월까지 공소시효라고...
-
수1수2확통 포함해서 2월부터 3월까지 한달만에 끝내려는데 물리적으로 가능한가요
-
흠냐뇨잇.
-
몇십분동안 찾아다니던 차 탈취해서 돌아다니고 있는데 ㅈ같은 광고 뜨더니 x표 눌러도...
-
왜 카메라 마사지를 받으면 점점 더 예뻐지고 멋있어지는가 0
긍정적이든 부정적이든 지속적으로 외모와 패션에 대한 피드백을 받기 때문임 그런...
-
십새들아.
-
괜찮아 문장 -> 기출정식 괜찮아 문장 -> 믿어봐 문장 -> 기출정식 뭐가 좋을까요
-
전적대(예정) 통학하긴 개빡센 거리인데 (불가능은 아님 근데 편도 2시간임) 기숙사...
-
패션 어렵구나 2
기본템부터벅벅하는중
-
학군지일수록 재수삼수는 기본으로 깔고 가는 애들이 태반인거 같음.. 삼수 사수는...
-
반도체 국가핵심기술 유출 시도 11명 기소…중국서 돈 받아 1
삼성전자가 개발한 국가핵심기술을 도용해 제작한 반도체 세정장비를 중국기업에...
-
ㅋㅋㅋㅋㅋㅋㅋㅋㅋ
-
내 인증은 사실 남친 얼굴임 이제야 밝힘
-
지하철보다 버스가 더 자주다니는 느낌임 아까전에 일산동구청 정류장 서있었는데 버스...
-
신남성연대 5
한때는 재밌게 봤는데 오랜만에 보니까 왜 이렇게 됐냐 증거인멸에 눈 귀 막고 채팅창...
-
워윅이 밴더임? 1
???
-
일단 코돈이 1타먹을듯
-
제자야 반응해라 14
ㅇ. 오늘은 또 뭐하면서 시간 보내지
-
님들 이거왜이럼 2
책 요즘 자꾸 이따구로 휘는데 대체 이유가….개빡침 원래 안이랬는데 겨울철이라...
-
고양이 0
가끔 심심하면 와서 앵김
















































